IP Bölüm 2 | Sayı Sistemleri Bölüm 1
Değerli arkadaşlar, merhaba! Bu yazımızda sizlerle, ‘Sayı Sistemleri’ hakkında konuşacağız. Bu yazıyı IP adresleri blogunun devamı olarak nitelendirebilirsiniz; IP adreslerine bağlı olan birkaç blog daha yayınlayacağız. Bu blogu, temiz ve sakin bir kafayla okumanızı önerebilirim.
Şimdi, bizim ilgilendiğimiz kısım aslında ‘Binary’ sayı sistemidir ama Binary sayı sistemini daha iyi anlamak adına onları, ‘Decimal’ sayı sistemleri ile birleştirerek anlatacağız. En son kısımda da 'HexaDecimal' kavramını anlatacağız.
Binary sayı sistemi, ‘1’ ve ‘0’lardan oluşan sayı sistemine verilen isimdir, Türkçe karşılığı ‘İkili Sayı Sistemi’ şeklindedir. Decimal sayı sisteminde ise durum biraz farklı. Burada, 0 ile 9 (dahil) arasındaki rakamlarla istenen sayılara ulaşabilmemizi sağlayan sisteme Decimal sayı sistemi adını veriyoruz ve bunu Türkçe’ye, ‘Onluk Sayı Sistemi’ olarak çevirebiliriz.
Bilgisayarlar, Ağlar gibi teknolojiler, ikili sayı sistemi ile çalışır. Dolayısıyla her şeyin nasıl çalıştığını anlayabilmemiz için ilk önce bu konuyu anlamamız gerekiyor. Ortaokul dönemlerinden eğer hatırlıyorsanız açık – kapalı devreler diye bir konu vardı. Bu konuda ‘anahtar’ dediğimiz yapı eğer açıksa buna ‘açık devre’ (yani sistem çalışmaz), eğer kapalıysa kapalı devre (yani sistem çalışır) derdik. Hatırlatıcı görsel:
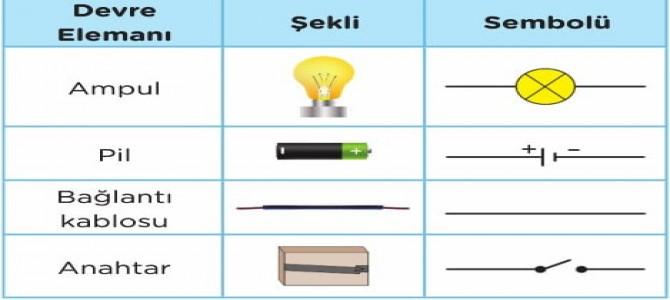
Bunun bir benzerini de bilgisayar ve ağ cihazlarında da görüyoruz. Eğer bir iletim söz konusuysa yani devre kapalı devreyse (anahtar kapalıysa) bunun karşılığı ‘1’ olacaktır. Eğer bir iletim söz konusu değilse yani devre açık devre ise (anahtar açıksa) bunun karşılığı da ‘0’ olacaktır. Kısaca, eğer veri iletişimi söz konusuysa yani kablo elektrik alıyorsa ‘1’ değerini, veri iletişimi söz konusu değilse yani kablo elektrik almıyorsa ‘0’ olarak geçecektir.
Kullanılan her kablo ‘1’ ve ‘0’ olmak üzere iki değer alır yani 1 adet kablo kullandığımızda o kablonun alabileceği maksimum 2 değer vardır. 2 adet kablo kullandığımızda alabilecekleri toplam değer 4 olacaktır. Dolayısıyla kablo sayısını artırdıkça bu değerler daha da artacaktır ve 32 adet kablo kullanıldığında 4 milyar adete yakın sayı oluşturulabilir demektir. Bu da muazzam bir güç demek oluyor.
İki adet kablo kullanımında oluşabilecek durumlar:
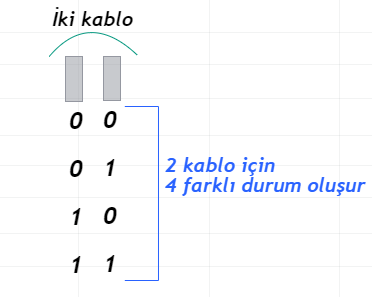
Şimdi, işin pratik kısmına gelelim. Sayı sistemlerini daha iyi anlamak için onları parçalamayı öğrenmeniz, nasıl hesaplandıklarını görmeniz elzemdir. Bu yüzden ilk önce Decimal yani Onluk Sayı Sistemi üzerinden bir parçalama işlemi yapalım:
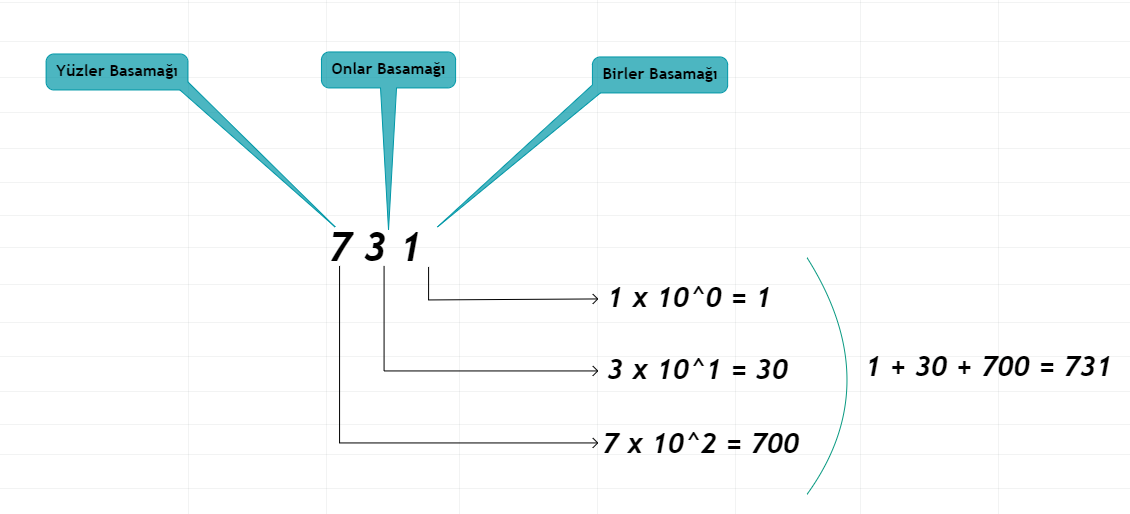
Birler, onlar, yüzler basamağı ve daha ilerisini biliyorsunuzdur. İşte bu noktada yukarıdaki sayıyı bölmeye başlıyoruz. Dikkat edin; birler basamağı ile ilgili işlemde;
Sayının
kendisi x 10 üzeri 0 = sonuç
şeklinde bir işlem yapmışız. Yukarıdaki örnek Decimal Sayı Sistemi örneği olduğu için her işlemde 10 tabanını kullanarak işlem yapıyoruz. 3 sayısı yani onlar basamağı için de aynı mantıkla işlem yapıyoruz fakat basamak sayısını artırdıkça üs kısmını da bir artırıyoruz. Yani;
Birler
basamağı için 10 üzeri 0 (10^0)
Onlar
basamağı için 10 üzeri 1 (10^1)
Yüzler
basamağı için 10 üzeri 2 (10 ^2) şeklinde işlem yapıyoruz. Eğer bu sayı 4, 5 veya daha fazla basamağa sahip olsaydı aynı işlemleri, üs kısmını bir artırarak yapacaktık.
Şimdi dilerseniz Binary sayı sistemini parçalamayı görelim:
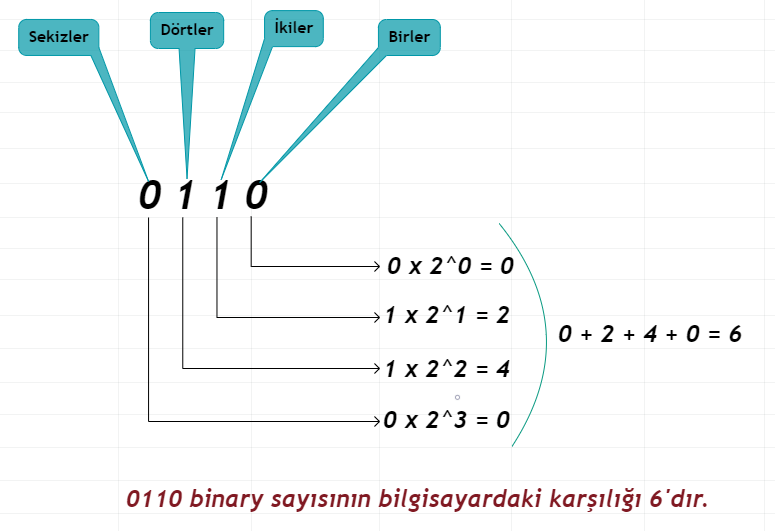
Yukarıda görüğünüz şey, Binary (ikili) sayı sisteminin parçalanış şeklidir. Az önce Decimal sistemde her şey 10 tabanından hesaplanıyordu ve Decimal’in Türkçe karşılığı ‘Onluk Sayı Sistemi’ idi. Burada ise her şey 2 tabanına göre hesaplanıyor. Dolayısıyla Türkçe karşılığı ‘İkili Sayı Sistemi’dir. Basamakların bölünme şekline dikkat edin; birler, ikiler, dörtler, sekizler. Az önce her basamak bir önceki basamağın 10 katı iken Binary sistemde her basamak bir önceki basamağın iki katı şeklinde ilerler.
İşlem yapma kısmına geldiğimizde ise işlemin tamamen aynı olduğunu, sadece tabanın değiştiğini görüyoruz. Birler basamağı için 2^0, ikiler basamağı için 2^1 ve diğerleri de üs kısmı bir artarak devam ediyor.
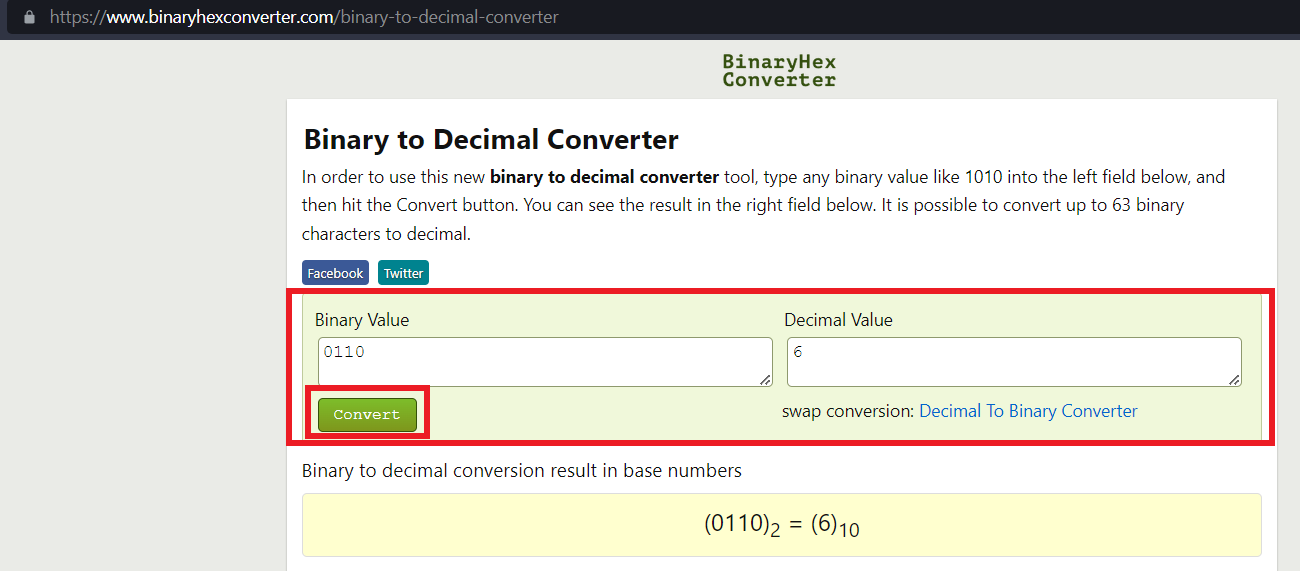
Biz, 0110 sayısının ne olduğunu bilmiyoruz. İşte bu matematik işlemini, bunun ne olduğunu anlamak için yapıyoruz. İşlemler sonucunda çıkan her sayıyı topluyoruz ve karşımıza çıkan sayı, Binary sayı sisteminde verilen sayının karşılığı oluyor. Yukarıdaki örnekten yola çıkarak diyebiliriz ki: “Biz bilgisayara 6 rakamını girdiğimizde bilgisayar arka planda bunu 0110 olarak anlıyor.”
Dilediğiniz Binary sayısının karşılığını bulabilmek için internete ‘Binary to Decimal’ tarzında bir arama yaparsanız birçok sonuçla karşılaşacaksınızdır. Yukarıdaki işlemi teyit etmek için ben de bir site buldum: Site linki için tıklayın.
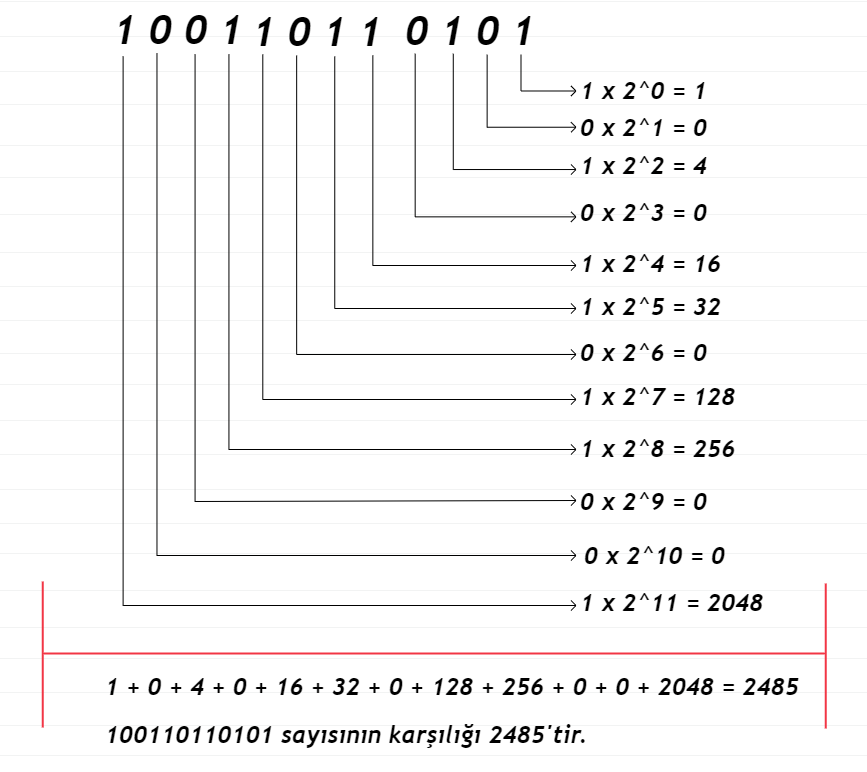
Decimal sayı sisteminde 4, 5 ve daha fazla basamağı da parçayabileceğimizi söylemiştik. Elbette bu kural, Binary sistem için de geçerlidir. Yani 0110 yerine 1001 1011 0101 gibi bir Binary sayısını da çözümleyebiliriz. Hatta yapalım:
Şimdi, bu konunun IP adresleriyle olan ilişkisini görelim. IP (Internet Protocol) adlı blogumuzda da bahsettiğimiz gibi bir IPv4 adresi, 32 bitten oluşur, 4 oktete ayrılır ve her oktet 8 bitten oluşur. 8 bit, 0 ile 255 arasında değerler alabilir. Yani bir IP adresinin her okteti 0-255 arasında değerler alabilir çünkü her oktet 8 bitten oluşur. Aşağıdaki tabloyu referans alalım. Buna göre eğer 11111111 şeklinde bir binary sayısı yazarsak bunun karşılığı; 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 işleminden 255 olarak çıkacaktır. Eğer hepsini 0 olarak yani 00000000 şeklinde bir binary sayı yazarsak bunun da karşılığı elbette 0 olacaktır. Bu da, IPv4’ün aralığı demek oluyor.
|
Bit |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Binary |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Üs |
2^7 |
2^6 |
2^5 |
2^4 |
2^3 |
2^2 |
2^1 |
2^0 |
|
Decimal |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Yukarıdaki tabloyu isminiz gibi bilmelisiniz. Blogun başında da dediğimiz gibi eğer bir veri alışverişi varsa bu ‘1’ ile, yoksa ‘0’ ile işaretlenir. Bir Binary’nin karşılığı 1 ise ona karşılık gelen Decimal değer ile işlem yaparız ama eğer bir Binary’nin karşılığı 0 ise Decimal değerini almayız. Örneğin 8 bitlik bir Binary sayımız olsun: 11001010
Biz bu Binary sayısını tabloya yerleştirdiğimiz zaman 1’e karşılık gelen Decimal sayıları toplayacağız; çünkü akım geçiyordur. 0’a karşılık gelen Decimal sayıları ise işleme dahil etmeyeceğiz; çünkü akım yoktur.
|
Bit |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Binary |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
Üs |
2^7 |
2^6 |
2^5 |
2^4 |
2^3 |
2^2 |
2^1 |
2^0 |
|
Decimal |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Tabloya göre yeşil kısımlarda akım vardır (1), kırmızı kısımlarda akım yoktur (0). O zaman;
11001010 Binary sayısının karşılığı => 128 + 64 + 8 + 2 = 202’dir diyebiliriz.
Hemen bir başka örnek yapalım ve bu sefer Binary sayımız ‘00110110’ olsun. Bu rakamları tek tek, ait oldukları yerlere yazıyoruz.
|
Bit |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
Binary |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
Üs |
2^7 |
2^6 |
2^5 |
2^4 |
2^3 |
2^2 |
2^1 |
2^0 |
|
Decimal |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Dediklerimizi tekrar hatırlayalım: “1 rakamına karşılık gelenleri toplayacağız, 0 rakamına karşılık gelenleri ise işleme dahil etmeyeceğiz.” Dolayısıyla;
00110110
Binary sayısının karşılığı => 32 + 16 + 4 + 2 = 54’tür diyebiliriz.
[*] Bu blog yazısını, teknik aksaklıklardan dolayı iki bölüme ayırdık. İkinci bölüm için tıklayın: https://blog-cyberworm.com/blog/sayi-sistemleri-2
Yayınlanma Tarihi: 2022-07-16 00:24:37
Son Düzenleme Tarihi: 2022-07-31 20:13:34
