IP Bölüm 2 | Sayı Sistemleri Bölüm 2
[*] Birinci bölüme dönmek için tıklayın: https://blog-cyberworm.com/blog/sayi-sistemleri-1
Şimdi, Binary’den Decimal’e dönüşümlerimizi yaptık. Peki ya Decimal’den Binary’e nasıl dönüşüm yapacağız? IP adlı blogumuzda verdiğimiz IP adresinin Binary karşılığını bulalım:
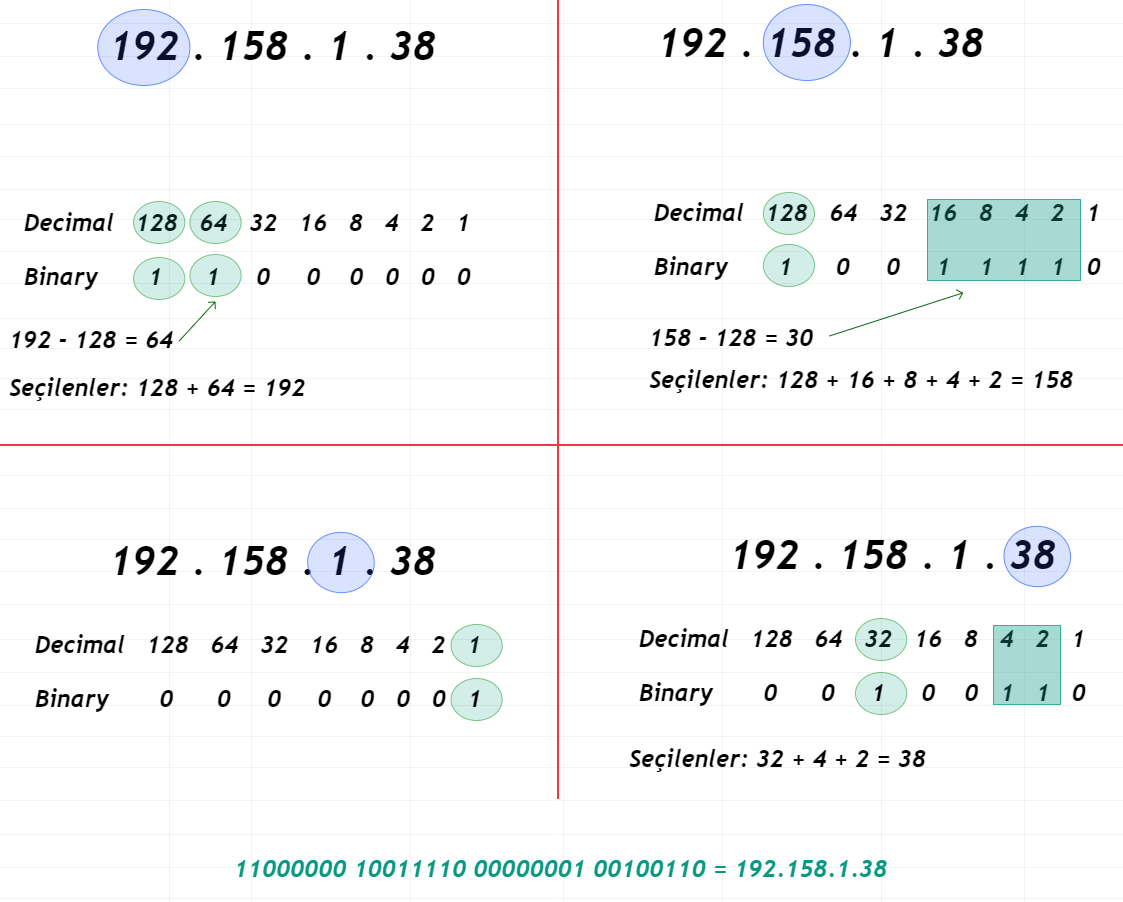
Şimdi, yukarıdaki görseli açıklayalım. Hedefimiz, bir IP adresinin Binary karşılığını bulmaktı. Bunun için ilk önce ‘192’ sayısından başladık. Tabloyu gözünüzün önüne getirin; orada 128’e kadar olan sayıları görüyorduk ama burada 192 sayısı var ve bu sayı 128 sayısından büyük; ne yapacağız?
Elbette 128 sayısını 1 olarak alacağız yani işleme dahil edeceğiz. Yani eğer 128’den bile büyük bir sayıyı dönüştüreceksek 128 sayısını 1 olarak alırız. Daha sonra işlem yapabilmemiz için bize verilen sayıdan 128’i çıkarırız. Yani 192 – 128 = 64 yaparız. Bulduğumuz sonucu, tabloda kalan verilere bakarak çıkarmaya çalışırız. Sormamız gereken soru şu: “Sonuç 64 çıktı; tabloda hangi sayıların toplamı 64 yapar?”. Elbette tabloda halihazırda 64 sayısı var olduğu için direkt olarak 64’ü alıyoruz yani ona 1 değerini verip işleme dahil ediyoruz. İşleme alacağınız sayıların toplamı, dönüştüreceğiniz sayıya eşit olmalıdır. Dikkat ettiyseniz işleme dahil ettiğimiz sayıların toplamı dönüştürdüğümüz sayıya eşit yani 128 + 64 = 192. Dolayısıyla artık diğer verilere ihtiyacımız kalmadı ve onlara 0 değerini vererek işleme hiç dahil etmedik. Bunun sonucunda ortaya çıkan Binary sayımız: ‘11000000’
Şimdi 158 sayısını Binary şeklinde göstereceğiz. Az önce dediğimiz gibi; eğer dönüştürülecek sayı 128’den büyükse 128 sayısını hemen 1 yapıyoruz ve onu işleme dahil ediyoruz; yaptık. Daha sonra yolumuzu daha net görebilmemiz için dönüştüreceğimiz değerden 128 değerini çıkarıyoruz; 158 – 128 = 30. Sonucumuz 30 olarak geldi. Peki, tabloda hangi sayıların toplamı 30 eder? Elbette 16 + 8 + 4 + 2 = 30. Dolayısıyla o değerleri de ‘1’ konumuna getirerdik ve işlemimiz tamamlandı. Hemen bunun sağlamasını yapalım: 128 + 16 + 8 + 4 + 2 = 158. İşlem doğru. Bunun sonucunda ortaya çıkan Binary sayımız: ‘10011110’
Şimdi sıra 1 sayısının Binary karşılığını bulmakta. Bunun için yapmamız gereken şey çok basit. 1 rakamı ne 128’den büyüktür ne de bulunmayacak bir rakamdır. Tablonun en sağında zaten yer aldığı için sadece o kısmı ‘1’ olarak alıp diğer bütün kısımları ‘0’ olarak alırız ve karşımıza çıkan Binary sayısı şu şekilde olur: ‘00000001’
Son olarak IP adresimizin son oktetinde bulunan 38 sayısının binary karşılığını bulalım. Bunun için yapmamız gereken şey, sayının 128’den büyük olup olmadığını kontrol etmektir. Sayı, 128’den büyük değil yani onu tablo içerisinde rahatça bulabiliriz. Hemen bakalım; hangi sayıların toplamı 38 ediyor? Elbette 32 + 4 + 2 = 38 ediyor. Hemen 32, 4 ve 2 sayılarını ‘1’ olarak, kalan her şeyi de ‘0’ olarak alalım. Bunun sonucunda karşımıza çıkan Binary sayısı şu şekilde olacaktır: ‘00100110’
İşte IP adresi olarak bildiğimiz bu arkadaşımızın bilgisayar dilindeki karşılığı tam olarak şu şekilde karşımıza çıkıyor: ‘11000000 10011110 00000001 00100110’. Dilerseniz bu 8 bitlik alanları tek tek yani oktet oktet, az önce verdiğim siteden dönüştürüp teyit edebilirsiniz.
Dilerseniz şimdi, '11000000 10011110 00000001 00100110' Binary sayısını oktet oktet ayırarak Decimal'e dönüştürelim yani IP adresimizi geri alalım.

Önce Decimal tablomuzu yazdık. Daha sonra oktette yer alan Binary sayılarını yazdık ve hangi sayılar 1’e denk geliyorsa o sayıları işleme aldık; çıkan sonuç, oktetimizin sonucuydu (Üçüncü oktette yeşil kutu içerisinde bulunan 0, 1 olmalı; yanlış yazmışım).
Şimdi, ihtiyaç sıralamasına bir bakalım ve teknolojinin harikalığını görelim: Binary sistemler ile bir IP adresini yazabilir ve ona erişebilir durumdaydık fakat her 32 bitlik IP adresinin Binary sayısını aklınızda tutmanız mümkün değildir. Bu sorunu aşabilmek adına IP adresi denen bir teknoloji yaratıldı. Daha kısa ve daha anlaşılırdı fakat yine de akılda tutması epey zordu. Bu sorunu da aşmak için DNS teknolojisi geliştirildi ve artık ne Binary sayılarını ne de IP adreslerini ezberlememize gerek kaldı. Teknoloji çok güzel bir şey, öyle değil mi?
Bunları iyi bir şekilde öğrenmek için lütfen birçok pratik yapın.
HexaDecimal
Evet, IPv4 adresleri ile ilişkilendirdiğimiz sayı sistemleri yüzünden IPv6 ve MAC adresleri bize kızmış. Bu yüzden de HexaDecimal kavramının ne olduğundan, IPv6 ve MAC adresi ile olan ilişkisinden bahsetmezsek olmaz.
HexaDecimal, Türkçe karşılığı ‘Onaltılı Sayı Sistemi’ olan başka bir sayı sistemi çeşididir. Binary’yi ikili sayı sistemi, Decimal’i onlu sayı sistemi şeklinde adlandırırken sürekli ya ‘1’ ve ‘0’ ya da 0 ile 9 arasında işlem yaptık. Burada, 0 ile 15 (toplam 16 karakter) arasında işlem yapacağız ama ‘9’ rakamından sonra devreye harfler girecek. Bildiğiniz üzere IPv4’ler sadece sayılardan oluşuyor fakat IPv6 ve MAC adresleri, içerisinde harf de barındırabiliyor. Ki bu, gayet güzel bir teknoloji olup daha fazla cihazın kullanılmasına olanak sağlıyor. MAC adresleri blogumuzu şuradan okuyabilirsiniz. Aşağıdaki tablo, Hexadecimal karakterlerin Decimal karakterlerce karşılığının ve ikisinin de Binary karşılığının ne olduğunu anlatıyor. Yani örneğin ‘0111’ Binary sayısı hem Decimal hem de HexaDecimal olarak 7 rakamını temsil ederken ‘1111’ Binary sayısı Decimal olarak 15 sayısını temsil eder ve HexaDecimal olarak ‘F’ harfini temsil eder.
|
HexaDecimal |
Decimal |
Binary |
|
0 |
0 |
0000 |
|
1 |
1 |
0001 |
|
2 |
2 |
0010 |
|
3 |
3 |
0011 |
|
4 |
4 |
0100 |
|
5 |
5 |
0101 |
|
6 |
6 |
0110 |
|
7 |
7 |
0111 |
|
8 |
8 |
1000 |
|
9 |
9 |
1001 |
|
A |
10 |
1010 |
|
B |
11 |
1011 |
|
C |
12 |
1100 |
|
D |
13 |
1101 |
|
E |
14 |
1110 |
|
F |
15 |
1111 |
IPv6 örneği: 3002:0bd6:0000:0000:0000:ee00:0033:6778
MAC örneği: 90:00:4E:87:BF:3C
HexaDecimal kavramını öğrenmek için isterseniz önce eski bilgilerimizi tazeleyelim. Binary sayısını Decimal'e dönüştürürken 1 ile 128 arasında bulunan tabloyu alıyorduk, karşılığı '1' olan sayıyı işleme dahil ediyorduk. Örneğin: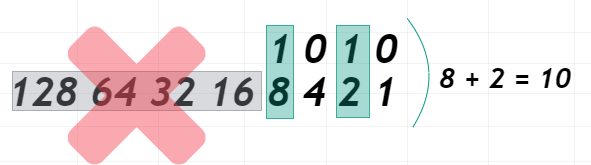
Bunu artık yapabilecek yetkinlikteyiz fakat HexaDecimal karşılığını nasıl bulacağız? Onun için sadece yukarıdaki tabloda verdiğim harfleri aklınızda tutmanız yeterli olacaktır; zaten alfabetik sıraya göre gittiği için kolayca anımsayabilirsiniz. Bulmak için de onları sırayla yazın ve karşılık gelen ifadeyi bulun:
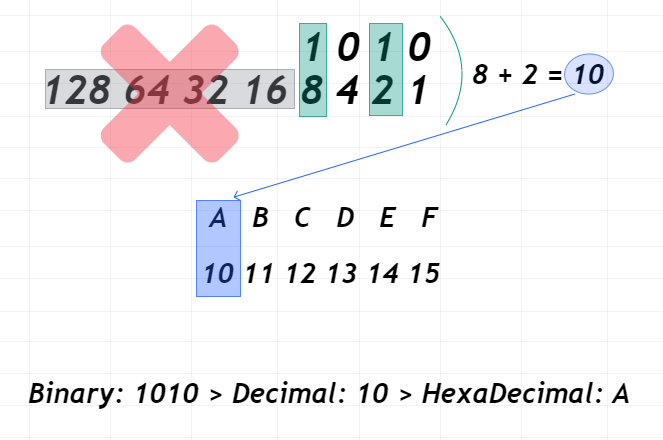
Az önce IP adresini Binary’e, ondan sonra tekrar Decimal’e dönüştürmüştük. Şimdi dilerseniz, IP adresini HexaDecimal’e dönüştürelim. Ben IP adresinin ilk iki oktetini yapacağım, kalan iki okteti siz yapmayı deneyin lütfen.

Yukarıda, Decimal olan bir veriyi (192) Binary sayı sistemine göre yazdık ve ortaya çıkan 8 biti ortadan ikiye böldük (yeşil ve mavi kutucuklar). Ayırdığımız bu kısımların karşılığına az önce verdiğim tablodan sırasıyla baktık ve sonucu bulduk. Ancak, dikkat ederseniz yeşil taraftaki 4 bitlik veriyi yapmakta zorlanıyoruz. Bunun için iki adet 4 bitlik verimizi de 8, 4, 2, 1 kısmında ölçüp biçmemiz gerekiyor.
Yani örneğin 192 sayısının Binary karşılığı 11000000 ise bunu ikiye bölüyoruz; 1100 0000. Sonrasında tablonun ikinci yarısını dikkate alıyoruz. Yani ilk önce 1100 kısmını 8, 4, 2, 1 bölümüne göre inceledikten sonra 0000 kısmını da 8, 4, 2, 1 bölümüne göre inceliyoruz. Bu durumda ilk 4 bitlik verimiz olan 1100 ifadesini 8, 4, 2, 1 bölümüne yerleştirirsek 8 ve 4'ün 1'e karşılık geldiğini, kalanların 0 olduğunu görebiliriz. Dolayısıyla 8 + 4 yaparız ve sonucu 12 olarak buluruz. Hex'e baktığımızda 12'nin karşılığının C olduğunu görüyoruz.
Hemen sonrasında ikinci 4 bitlik veriyi de aynı yere yerleştiriyoruz; 0000 : 8,4,2,1. Hepsi 0 olduğundan bu değeri 0 olarak almamız gerekiyor. Sonucumuz ise C0 şeklinde gelecektir.
158 sayısı için de anlatımımızı yapalım. 158'i Binary'e dönüştürdüğümüzde karşımıza 10011110 şeklinde bir veri çıkıyor. Bu 8 bitlik veriyi ikiye bölmemiz lazım; 1001 1110. Bunu da yaptıktan sonra iki parçayı da tablonun ikinci yarısına yerleştiriyoruz. Yani;
8 4 2 1
1 0 0 1
Bunun karşılığında 8 + 1 yapmamız lazım çünkü değerleri 1'dir. İlk 4 bitlik verimizin değeri 9.
8 4 2 1
1 1 1 0
Burada ise 8 + 4 + 2 yapmamız lazım çünkü bu değerler 1'e tekabül etmekte. Sonucumuz 14 gelecektir ama bunun Hex karşılığı da E olacaktır. Dolayısıyla 158'in Hex karşılığı 9E olacaktır.
Evet, blogumuzun sonuna geldik, bir şey daha söylemek istiyorum. Decimal yapıda olan bir sayıyı Binary sayı sistemine dönüştürmek için az önce anlattıklarım dışında bir yöntem daha vardır. Bu yöntemde, sayıyı sürekli 2’ye bölüyorsunuz ve kalan sayıyı tutuyorsunuz. Sayı, 2’ye bölünemeyecek düzeye gelene kadar bu işlemi tekrarlıyorsunuz. Daha sonra kalanları tersten alıp yan yana yazıyorsunuz ve ortaya Binary çıkmış oluyor. Fakat ben bu yöntemi kesinlikle önermiyorum çünkü hem çok uzun sürebilir hem de ileride eğer ciddi sertifika sınavlarına girerseniz bu yöntem size çok zaman kaybettirecek ve kafanızı karıştıracaktır. Bu yöntemle ‘192’ sayısını Binary sayı sistemine çevirmeye çalışın, ne demek istediğimi anlayacaksınız. Elbette, eğer sadece öğrenmek istiyorsanız buna da bakabilirsiniz. Detaylarını internetten bulabilirsiniz ve aşağıda bir örneğini görebilirsiniz (yazının çirkinliği için kusura bakmayın 😊):

Yayınlanma Tarihi: 2022-07-16 00:42:29
Son Düzenleme Tarihi: 2024-06-11 10:18:34
